Activity 4.4 Mathematical Modeling Part 2 Answers

Critical Path Method (CPM) is a project schedule modeling technique. Mr. Morgan R. Walker and James E. Kelly developed this technique in the late 1950s.

Project planners use this method to develop schedules for projects, including IT, research, and construction.

Critical Path Method is a lengthy and complex concept. Please follow each step in this blog post, and don't move on until you understand the previous steps. If you follow this advice and complete the blog post, you won't have any problems solving Critical Path Method questions on the PMP Exam.

Critical Path Method

In the critical path network method, you focus on managing the critical path.

A network diagram has many paths originating from one point and ending at another point. Every path has a duration, and the one with the longest duration is the critical path.

You can define a critical path as:

The longest path in the network diagram, or
The shortest duration to complete the project.

Notice that the first statement talks about the longest path, and the other talks about the shortest duration.

They may appear to be opposites, but they are conveying the same message.

For example, let's say you have a project to construct three buildings. The first is the largest, the second is medium-sized, and the third is the smallest.

You develop the network diagram, which comprises three paths, each representing a building.

You calculate the duration for each path. For the first building, the duration is 31 months, the second will take 18 months, and the third will require 13 months.

You can see that the first path is for the largest building, the second path is for the medium-sized one, and the third path is for the smallest building.

Now, let us review the diagram for the critical path analysis.

Did you notice that the first path is the longest?

It is 13 months longer than the second and 18 months longer than the third.

This means that you can wait 13 months and then start working on the second building because you can complete the second building in 18 months.

Likewise, you could wait 18 months and then start working on the third building because it will take 13 months to complete. This means that, even if you start work on the third building after 18 months from the project start date, you can finish it on time.

This waiting period is known as the float or slack.

So, which is the critical path in this network diagram?

It is the longest path on the network diagram because you cannot complete your project before finishing the first building. Although you can complete the other two buildings quickly, your project is not considered complete until the first building is completed.

This confirms the first statement that says, "the critical path is the longest path on the network diagram."

Now, what is the shortest duration to complete the project?

It is 31 months because you cannot complete your project in less time, and this is the duration of the critical path.

This bears out the second statement that says, "The critical path is the shortest duration in which you can complete the project."

So, both definitions are the same.

You can define the critical path as the sequence of activities from start to end, and it has the longest duration of all paths in a network diagram.

In ideal conditions, a network diagram should have one critical path. Multiple critical paths will put you in a difficult situation.

The critical path has the longest duration, and it is the total project's duration. Activities on the critical path have no float; therefore, you must ensure those critical activities are completed on time. Any delay in a critical activity (critical path activity) will delay the project.

What if the project is delayed?

Schedule slippage is common in project management. However, some tools can help you bring things back on schedule. These are called schedule compression techniques, and Fast-tracking and Crashing are two examples. If your project is behind schedule, you can use these tools to get it back on time.

Visit: Fast Tracking and Crashing

A Few Commonly Used Terms in Critical Path Method

Before I start discussing how to find the critical path, let us understand a few common terms used in a critical path network diagram:

Earliest Start Time or Early Start (ES): This is the earliest time an activity can be started in your project.

Latest Start Time or Late Start (LS): This is the latest time that an activity can be started on your project. If you start the activity beyond this time, it will affect your critical path.

Earliest Finish Time or Early Finish (EF): This is the earliest time an activity is completed in your project.

Latest Finish Time of Late Finish (LF): This is the latest time you can complete the activity on your project. If your activity crosses this time, your project will be delayed.

How to Find the Critical Path in a Network Diagram

Now we have reviewed critical path method terminology, let's see how we can calculate the critical path, late start, early start, late finish, and early finish:

The first step is to collect all project activities. You can use the work breakdown structure to find tasks for your project.
After listing project activities, find the task dependencies among the activities. Find which activity will follow what activity and task relationship such as finish to start, finish to finish, start to start, or start to finish.
Now, draw the network diagram and assign durations to each activity.
Identify all paths in the network diagram.
Find the duration of each path.
The path with the largest duration is the critical path.
Use forward pass the calculate the earliest start or early start, and earliest finish or early finish of each activity.
Use backward pass the calculate the latest start or late start and the latest finish or late finish for each activity.
Now you can calculate the float for all activities.
Note that on a critical path, a late start will be equal to a late finish, and an early start will be equal to a late start. Also, all critical path activities will have no float.

This information lets you draw the critical path network diagram, and you will know the float of each activity. You will how much you can delay a particular task, and any delay beyond this point will affect the project schedule.

Critical Path Method Example

Based on the network diagram below, identify the total paths, critical path, and float for each path.

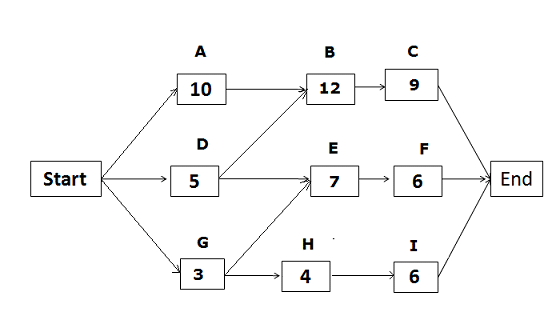
The above network diagram has five paths. The paths and their durations are as follows:

Start -> A -> B -> C-> End {duration: 31 days.}
Start ->D -> E ->F -> End {duration: 18 days.}
Start -> D -> B -> C -> End {duration: 26 days.}
Start -> G ->H ->I -> End {duration: 13 days.}
Start -> G -> E ->F -> End {duration: 16 days.}

Since the duration of the first path is the longest, it is the critical path. The float on the critical path is zero.

The float for the second path "Start ->D -> E ->F -> End" = duration of the critical path – duration of the path "Start ->D -> E ->F -> End"

= 31 – 18 = 13

Hence, the float for the second path is 13 days.

Using the same process, we can calculate the float for other paths as well.

Float for the third path = 31 – 26 = 5 days.

Float for the fourth path = 31 – 13 = 18 days.

Float for the fifth path = 31 – 16 = 15 days.

Calculate Early Start, Early Finish, Late Start, and Late Finish

We have identified the critical path and the duration of the other paths. Now it's time to move on to more advanced calculations: Early Start, Early Finish, Late Start, and Late Finish.

Calculating Early Start (ES) and Early Finish (EF)

To calculate the Early Start and Early Finish dates, we use the forward pass; we will start from the beginning and proceed to the end.

The Early Start (ES) for the first activity on any path will be 1 because you cannot start the activity before the first day of your project.

The starting point for any activity is the endpoint of the predecessor activity on the same path (plus one).

The formula used for calculating Early Start and Early Finish dates:

Early Start of the activity = Early Finish of predecessor activity + 1
Early Finish of the activity = Activity duration + Early Start of activity – 1

Early Start and Early Finish Dates for the path Start -> A -> B -> C -> End

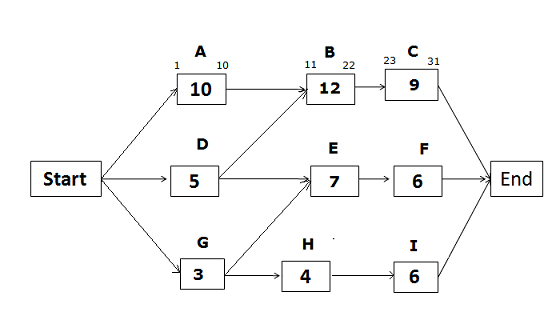
Early Start of activity A = 1 (Since this is the first activity of the path)

Early Finish of activity A = ES of activity A + activity duration – 1

= 1 + 10 – 1 = 10

Early Start of activity B = EF of predecessor activity + 1

= 10 +1 = 11

Early Finish of activity B = ES of activity B + activity duration – 1

= 11 + 12 – 1 = 22

Early Start of activity C = EF of predecessor activity + 1

= 22 +1 = 23

Early Finish of activity C = ES of activity C + activity duration – 1

= 23 + 9 – 1 = 31

Early Start and Early Finish Dates for the path Start -> D -> E -> F -> End

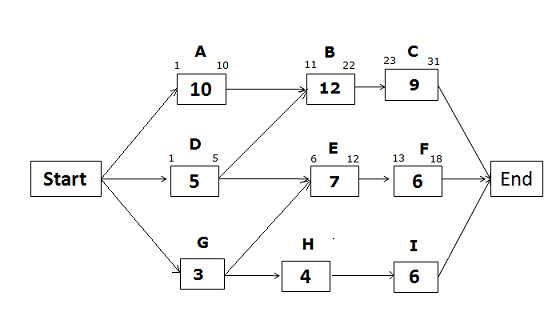
Early Start of activity D = 1 (Since this is the first activity of the path)

Early Finish of activity D = 1 + 5 – 1 = 5

Early Start of activity E = EF of predecessor activity + 1

Since activity E has two predecessor activities, which one will you select? The answer is the activity with the greater Early Finish date. The Early Finish of activity D is 5, and the Early Finish of activity G is 3 (we will calculate it later).

Therefore, we will select the Early Finish of activity D to find the Early Start of activity E.

Early Start of activity E = EF of predecessor activity + 1

= 5 + 1 = 6

Early Finish of activity E = 6 + 7 – 1 = 12

Early Start of activity F = 12 + 1 = 13

Early Finish of activity F = 13 + 6 -1 = 18

Early Start and Early Finish Dates for the path Start -> G -> H -> I -> End

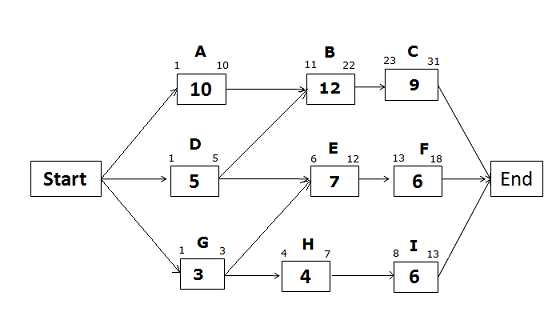
Early Start of activity G = 1 (Since this is the first activity of the path)

Early Finish of activity G = 1 + 3 – 1 = 3

Early Start of activity H = 3 + 1 = 4

Early Finish of activity H = 4 + 4 – 1 = 7

Early Start of activity I = 7 +1 = 8

Early Finish of activity I = 8 + 6 – 1 = 13

Calculating Late Start (LS) and Late Finish (LF)

We have calculated the Early Start and Early Finish dates of all activities. Now it is time to calculate the Late Start and Late Finish dates.

The Late Finish date of the last activity on all paths will be the same because no activities can continue once the project is completed.

The formula used for Late Start and Late Finish dates:

Late Start of Activity = Late Finish of activity – activity duration + 1
Late Finish of Activity = Late Start of successor activity – 1

To calculate the Late Start and Late Finish, we use the backward pass; i.e. we will start from the last activity and move back towards the first activity.

Late Start and Late Finish Dates for the path Start -> A -> B -> C -> End

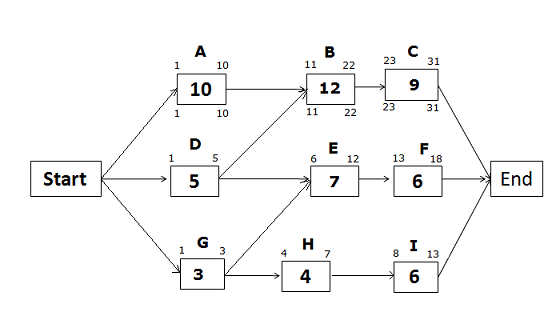
On a critical path, the Late Start, and Late Finish dates will be the same as the Early Start and Early Finish dates

Late Start and Late Finish Dates for the path Start -> D -> E -> F -> End

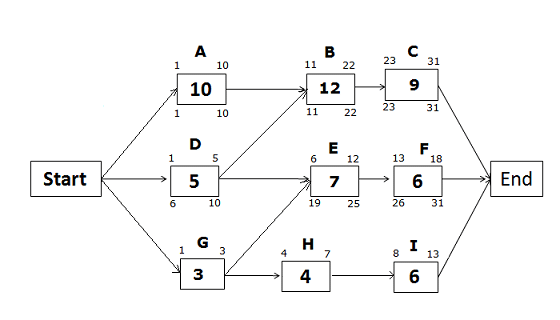
Late Finish of activity F = 31 (because you cannot allow any activity to pass the project completion date)

Late Start of activity F = LF of activity F – activity duration + 1

= 31 – 6 +1 = 26

Late Finish of Activity E = LS of successor activity – 1

= LS of Activity F – 1

= 26 – 1 = 25

Late Start of Activity E = LF of activity E – activity duration + 1

= 25 – 7 + 1 = 19

Late Finish of activity D = LS of successor activity – 1

If you look at the network diagram, you will notice that activity D has two successor activities, B and E. So, which activity would you select?

You will select the activity with the earlier (least) Late Start date. Here, the Late Start of activity B is 11, and the Late Start of activity E is 19.

Therefore, you will select activity B, which has the earlier Late Start date.

Hence,

Late Finish of activity D = LS of activity B – 1

= 11 – 1 = 10

Late Start of Activity D = LF of activity D – activity duration + 1

= 10 – 5 + 1 = 6

Late Start and Late Finish Dates for the path Start -> G -> H -> I -> End

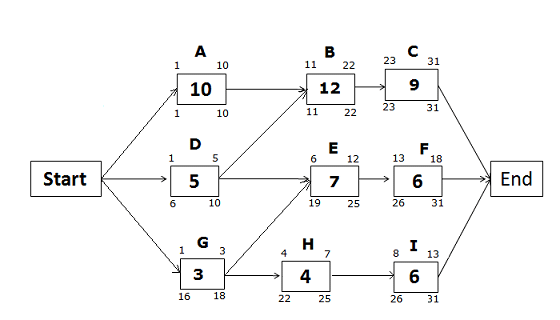
Late Finish of activity I = 31 (because you cannot allow any activity to pass the project completion date)

Late Start of activity I = 31 – 6 + 1 = 26

Late Finish of activity H = 26 – 1 = 25

Late Start of activity H = 25 – 4 + 1 = 22

Late Finish of Activity G = 19 – 1= 18 (we will choose the late start of activity E, not activity H because the Late Start of activity E is earlier than the Late Start of activity H).

Late Start of activity G = 18 – 3 + 1

= 16

Calculate the Free Float

I recommend that you read my blog post on the total float and free float to get a better understanding before proceeding further.

Visit: Total Float and Free Float

The formula for the Free Float is:

Free Float = ES of next activity – EF of current activity – 1

Benefits of the Critical Path Method

The following are a few benefits of the Critical Path Method:

It shows a graphical view of the project.
You can discover and visualize dependencies.
It aids in project planning, scheduling, and controlling.
It helps in contingency planning.
You can see the critical path and identify critical activities.
It helps you assign the float to activities and flexibility to float activities.
It shows you where you can take action to bring projects back on track.

Drawbacks of the Critical Path Method

Although the critical path is a very useful tool in project planning, it has some drawbacks, such as:

The Critical Path Method is an optimal planning tool and assumes that all resources are always available for the project.
It does not consider resource dependencies.
There is a chance of misusing float or slack.
Less attention is paid to non-critical activities, though sometimes they may become critical activities.
Projects based on the critical path often do not finish on time.
For complex project you will need to use project management software to develop the critical path scheduleing that will add cost to your project.

To overcome these shortcomings, the Critical Chain Method (CCM) was developed.

Visit: Critical Chain Method in Project Management

Apart from the CCM method, many project planners use schedule based on the Gantt chart.

Summary

The Critical Path Method has helped many project managers develop and manage schedules. It is a good communication tool, and it helps secure stakeholder buy-in. A network diagram has many paths, but you must focus on the critical one. Any delay in critical activity will affect the project schedule. Monitor floats on other paths because if the float drops to zero, that path will become a critical path, and you should avoid this.

As a project manager, you must monitor your network diagram and take prompt corrective action whenever necessary.

Are you involved with project planning? Please share your experience with the Critical Path Method in the comments section.

This is an important topic from a PMP exam point of view. You will see many questions in your exam on this topic.